Posted on

Laser Fizeau Interferometer History

The laser Fizeau interferometer has experienced several transformations from its original design. Like all evolutionary processes, some vestigial design elements remain in commonly used interferometers, which do not address and can impede measurements required to control and optimize today’s optical manufacturing processes.

Circa 1850: Fizeau Interferometer

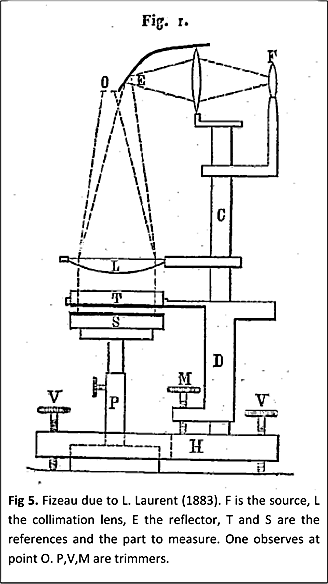
Armand Hippolyte Louis Fizeau (1819 – 1896)  invented the interferometer configuration, now named after him, for measurements of glass parameters which he presented at the French Academy of Sciences in 1862. Earlier, in 1851 he used a version of this interferometer in his famous experiment devised to test the ether-drag theory. The results seemed to support a partial ether-drag, that were later confirmed by Michelson and Morley. In a twist of fate the ether theory was disproved shortly after by the more famous Michelson-Morley experiment, but the results of BOTH of these experiments lead the way to Einstein’s theory of relativity. “Einstein later pointed out the importance of the [Fizeau] experiment for special relativity, in which it corresponds to the relativistic velocity-addition formula when restricted to small velocities,” Wikipedia

Armand Hippolyte Louis Fizeau
1st Fizeau Interferometer

Pre-1960’s

Before the invention of the laser in the 1960’s optical test interferometers were difficult to use and often had to be custom built for each application.  Low-coherence illumination favored equal path interferometers like a Twyman-Green or Mach-Zehnder configuration. The Fizeau – though already commercially available – were large, very heavy, difficult to use and limited to measurements of flat surfaces.

The most popular interferometer, though rarely considered one, is the Test Plate using Newton’s Rings. A test plate is strikingly similar to a Fizeau configuration with only several micrometers of working distance. The test plate consists of one reference surface for each surface an a low coherence filtered source

 

Twyman-Green Interferometer
Test Plate

1960’s – The Laser becomes Practical

The laser made interferometry much easier to implement. “Bob Hopkins…was quick to realize how much the laser could be used to improve the testing of optical components” (J.C. Wyant, “Short history of interferometric metrology”). With the laser, fringes were easy to find making interferometry a practical tool supporting optical manufacture. Much progress was made in testing configurations, yet interferometry remained an experts tool, custom made for the application and developed and run by engineers and scientists. Plus to use a HeNe laser, the most widely available required stabilizing it to have only one frequency of output. Low cost unstablized HeNe lasers had short coherence, around 200 mm and were limited to use in a Twyman Green configuration where the test and reference could be balance. These stabilized lasers were very expensive, in 2020 dollars they would cost $35,000!

The 1st HeNe Laser – Bell Labs (J. Hecht, “History of Gas Lasers, Part 1 Continuous Wave Gas Lasers”, Opt. Phot, January 2010)

1970’s – The Modern Fizeau Architecture is Created

What is now considered a Fizeau interferometer was created in the 1970’s by two different events: The invention of the modular Fizeau interferometer with a laser source, plus computerized phase measurements.

The Fizeau Optical/Mechanical Architecture

The HeNe laser promised to make interferometers much easier to use, but its cost blocked interferometers from becoming a commercial success. The key insight at Zygo that enabled the modern Fizeau interferometer design was that a simple polarizer in front of a multi-mode, low cost laser produced meters long coherence.  This insight was applied in 1972 by Carl Zanoni and George Hunter at ZYGO constructing  the GH (for George Hunter the principle designer) and the follow-on Mark II™ in 1976 when modern interferometry was born.

 

GH Interferometer: Transmission Sphere/Interferometer Architecture with Polaroid fringe capture
Mark II™ interferometer: Vidicon Tube Camera introduced for live fringe viewing

It is important to understand the architecture of the Mark II™ to know WHY interferometers are designed as they are today. The ZYGO innovations were a low cost, long coherence laser, a flexible optical architecture, a simple alignment system, with a clean fringe image. The architecture combines an interferometer (“mainframe” in ZYGO terminology in a nod to the 1970’s Tektronix Oscilloscope architecture) with quickly interchangeable reference lenses/reference-surfaces they named transmission spheres (TS) and transmission flats (TF).

With the long working distance due to long laser coherence one TS eliminated the need for large libraries of Test Plates – bringing cost savings and convenience. Plus Test Plates are used in virtual contact, separating the optical test surface from the reference surface eliminated the possibility of scratching and damage.

Ease of use was augmented by the alignment system. The twin spot alignment visually indicated when the cavity alignment was close enough for interference fringes to be found. Now non optical engineers could align and configure an interferometer.

The imaging system of Mark II™ REQUIRED a zoom lens to measure a wide range of part diameters since the only imager available was a vidicon camera. Both the zoom lens and the vidicon produced back reflections and secondary fringe patterns. The solution was a rotating ground glass, “coherence buster”, at an intermediate image that was then imaged incoherently through the zoom lens and onto the vidicon.

Zygo Mark II™ optical design architecture – from the patent drawing

Mark Interferometer Design Limitations

This design was so successful that even today’s interferometers with ground glass and 6X zoom are IDENTICAL to the optical system designed for the Mark II™. This is important to understand since the original optical system was designed for a vidicon camera AND only considered the visual measurement of spherical and flat optics manufactured with pitch polished processes.

If a megapixel camera is used in this design, the magnification by the zoom lens is empty, meaning resolution is not increased and potentially degraded. Further, imaging distortion of one or two pixels at 128X128 was acceptable but is problematic when spot polishing techniques are employed that require interferometer feedback for correction. These limitations lead to the development of fixed or stepped magnification imaging systems in the 2000’s, to be discussed later.

The historical influence of the Mark II™ optical architecture cannot be underestimated. All commercially successful interferometers follow the laser + “mainframe” + Transmission Reference architecture. Plus commercially successful alternative optical imaging design were only developed in the 2000’s, where even today (2018) historical inertia drives buying decisions.

The Data Acquisition System

Bell Labs patented computer data acquisition phase measuring interferometry. John Bruning and Donald Harriott’s group and Tropel (now CORNING) worked together to develop the a phase measuring system.

In the 1970’s Bell Labs was pushing the leading edge of semiconductor manufacturing technology. Lenses to support semiconductor manufacture were difficult to build due to their, at the time, extreme tolerances. Conventional visual or fringe center data analysis was not sufficient. Minicomputers were available and enabled in-the-lab data acquisition, as opposed to central batch processing of a few years earlier. Add to this signal processing was a core technology at Bell Labs. This combination enabled retrieving interferogram phase, pixel by pixel, an innovation that started the explosion of development that has continued until today.

Phase acquisition was achieved by changing the interference cavity length by λ/4, stopping, capturing a 32 X 32 sampled camera frame, moving another  λ/4 step, frame grab…until four camera frames were captured. A simple calculation eliminates the background intensity term and isolates the phase for each pixel. This is commonly called Phase Stepping Interferometry. Phase Stepping was used to minimize errors due to phosphor hysteresis.

TROPEL (CORNING) developed the first commercial computerized Phase Stepping systems. These were vertical laser interferometers that operated in the Twyman-Green and Fizeau mode. Data processing included a 32X32 array data acquisition off a vidicon tube camera.

A few years later Jim Wyant at WYKO introduced Phase Shifting, where a phase was continuously swept and not stepped, improving accuracy and measurement speed. This method was enabled by the use of CCD sensors.

1980’s – The Digital Age

Developments in the 1980’s centered upon improving data acquisition. In-fact data acquisition was the locus of improvements over the next 20 years. ZYGO became the dominant provider of interferometers with TROPEL deciding to concentrate on in-house development supporting ultra-high accuracy metrology and application focused systems (to be discussed later).

Digital Cameras

Digital cameras were now commercially available. The ZYGO Mark III™ had a 100 X 100 pixel array CCD and a home built board level computer with a frame grabber, with data acquired using a 4 frame data acquisition algorithm.

Vidicon Tube and CCD Imager

Software and Computers Enhance Performance

The second half of the 1980’s saw the development of the ZYGO Mark IV™ with a “high-density processor” system with a 256×256 array CID camera. The Mark IV HDP system was based on ZYGO’s own computer, computer operating system and internally developed Basic-like software language that was then scripted into a user interface. The software package allowed for custom scripting which required intensive software support. The software was slow and expensive to develop, difficult to use and quickly out of date.

Zygo® MarkVI Software User Interface

In the 1980’s Wyko Corporation emerged to commercialize the phase shifting microscope and then the Fizeau interferometer. WYKO was innovative regarding data acquisition and software. Based on commercially available computers, operating systems and development software, innovative uses of cameras and phase modulators, WYKO data acquisition systems evolved more quickly than ZYGO.

WYKO’s Innovation enabled the industry to quickly see the value of software to present easy to understand data and also employ algorithms to improve the quality and speed of data analysis.

Wyko 6000 Laser Fizeau Interferometer and software

These innovations include color plots, extended analysis in MTF, PSF, and Fourier based analysis that pushed the industry forward. 

This competitive pressure drove ZYGO to develop MetroPro™ the program which became the industry standard software for the next 25 years. MetroPro™ was based on Objective-C an early and quickly obsolete programming language. Yet using the object oriented software gave MetroPro™ the flexibility to survive all those years. 

The competition between WYKO® and ZYGO® benefited the optics community tremendously as they challenged each other to improve.

MetroPro™ Software

Innovation in the 1980’s

Wavelength Modulated PSI

Phase shifting data acquisition require the phase of the cavity to change. Changing the cavity OPL can be accomplish by slightly changing the wavelength [Gary  Sommargren], its commercial application was not fully implemented until 15 years later. (Note: cavity phase can also be modulated via phase modulating the source spectrum, see SCI in the 2000’s)

Vibration Insensitive Interferometry

Two significant inventions that would not become commercially successful until the 2000’s were invented in the 1980’s: Carrier fringe [Takeda, H. Ina and S. Kobayashi] and multi-camera frame simultaneous interferometry [Smythe & Moore]. Both of these enable phase measurement at microsecond rates enabling interferometry in vibrating and turbulent environments.

1990’s – Software and Computers Improve Performance

The Personal Computer revolution of the 1990’s and continuous improvements in semiconductor imaging (CCD’s) were the basis of most improvements in the 1990’s. The Mark II architecture was maintained and repackaged, while faster computers, improving software analysis and higher density cameras were added.

Algorithms

A new concentration on algorithms occurred. It was seen that a robust algorithm could compensate for errors in the data acquisition and environment. New multi-frame algorithms [Creath, Degroot] were created throughout this period.

In tangential fields of speckle interferometry, vibration correction algorithms were being developed that would find their way into Fizeau interferometry after 2000. These so called Vibration Tolerant PSI algorithms make Fizeau Interferometry more accurate in environments where data can be obtained but ripple appears in the data.

High Volume Manufacturing

The growth of high volume manufacture in Asia led to new entrants. The relative expense of WYKO and ZYGO systems positioned them in the market as the R&D and QC standards for wavefront measurement and Fujinon and Olympus emerged as the small aperture interferometers providers for surface and wavefront production measurement.

Molded optics, pioneered at KODAK in the USA in the early 1980’s, led to new consumer cameras and optical data storage devices driving the need for high volume asphere metrology. Interferometers were not able to measure these lenses or molds, leading to rise of stylus profilers from Taylor Hobson and Panasonic. It was not until the early 2000’s that interferometers were developed to measure aspheres.

Vibration Insensitive Commercial Interferometers Emerge

In the early 1990’s Dr. Michael Küchel, of Carl Zeiss, developed the Direct 100 laser Fizeau, a multi-wavelength optical interferometer with advanced optical architecture and data acquisition based on carrier fringe. Custom electronics acquired data at frame rates. The Direct 100 architecture is still employed today in some non-commercial applications. Phase Shift Technology also introduced a multi-camera interferometer on a custom basis. The expense of these interferometers limited their commercial success.

New Source Modality Discovered

A “White Light Fizeau Interferometer” was created by  Professor Schwider in 1997. The light source was a broadband source with spectral content. The unique result was interference fringes a fixed distance from the Fizeau reference surface.

Modern History

It is difficult to determine what are the “landmark” developments without the passage of time. For the last 18 years we will simply review some of the major technology and products introduced to solve a greater range of application via Fizeau interferometry

2000’s – Data Acquisition, Imaging, Illumination, Aspheres and Workstations

Deterministic optical manufacturing drove innovation in the interferometry market. The dominant manufacturing technique up to the 2000’s was pitch polished spheres and flats, which the old Mark II™ could handle. Now, new spot polishing computer controlled machines rendered the capabilities of old style interferometers insufficient. In order to keep pace with the advances in optical manufacturing, optical polishing production had to be capable of the following:

  • Minimizing image distortion for accurate positioning
  • Calibrating image size in order to know artifact position
  • Contain a high resolution optical system in order to detect the mid-spatial frequencies
  • The ability to produce sharp images all the way to the edge of the image in order to minimize coherent artifacts at the object’s edge
  • Measure very steep surfaces approaching hemispheres

 

CNC Polishing Drove the Need for Improved Fizeau Interferometers

Imaging Improvements

In order to accommodate the industry’s new demands, the Mark II type instruments had to be abandoned. Interferometers with fixed magnification and low distortion imaging, calibrated image size and high pixel resolution emerged. 

Workstations

Integrated workstations were developed primarily in Germany in order to move interferometers out of the quality control laboratory and next to the polishing equipment. The advantage of a workstation was the efficiency of integrating an interferometer directly into the production process to measure both surface form and radius of curvature easily and occupy as little floor space as possible. 

Commercial laser Fizeau workstation

Data Acquisition

Vibration Insensitive Commercially Viable

4D Technology introduced a Simultaneous Phase Measuring Interferometer (SPMI) that was the first commercially successful interferometer of its kind.  By combining the TROPEL 4-camera approach onto a single detector, the system became robust and easy to use [Novak et. al.]. The expanded manufacture of large mirrors for space and terrestrial application gave 4D Technology an application to establish their business and become a major player in the interferometry market.

4D Data Acquisition System: 1 Camera with 4 Phases

A different approach to eliminating vibration sensitivity was developed by ESDI [Szwaykowski et.al.], which introduced the concept of a spatially split source using a high coherency laser in a Fizeau interferometer. This allowed for the simultaneous capture of 3 phase-shifted interferograms.

Carrier Fringe data acquisition also became common as simple PC computers became fast enough to acquire and analyze data sets.

Scanning Fizeau Asphere

An asphere measuring interferometer was introduced by ZYGO. This was a scanning Fizeau [Küchel] that built up rings of data as the part scanned along its optical axis to measure each asphere zone. The zones were then combined to map the as much of the surface as could be accessed.

Scanning Fizeau Interferometer for Asphere Measurement

Stitching of Fast Convex Spheres & Aspheres

QED introduced a practical stitching system [Forbes et.al.] to measure steep, approaching hemispherical spheres. Beside more coverage of steep spheres, higher accuracy due to averaging and potentially higher spatial frequencies were being reported.

Light Source

Several modifications to the point source were introduced in the late 1990’s/early 2000’s which attempted to reduce diffraction artifacts caused by dust particles and other imperfections in the optical system of the interferometer. These were based mostly on increasing the size of the source by projecting a pattern using highly coherent light from the laser onto a rotating ground glass. Such sources with a decreased degree of spatial coherency can eliminate coherent patterns produced by diffraction on small particles and can be very effective, especially when such particles are located far away from the imaging plane. 

Scanning Laser Wavelength/Fourier Transform Acquisition

In order to handle measurements of optical components with parallel front and back surfaces, ZYGO introduced a tunable, coherent laser source [Deck] in which the wavelength of light can be swept in a controllable way. This innovation enabled analysis based on a Fourier transformation. Additionally, separate reflections from the front and back surfaces of the sample could be taken in one measurement, which allowed for independent measurements of those surfaces. This method also made it possible to take measurements of the sample optical thickness. This technique is limited to ~1.5 mm optical thickness, limited by the scanning range of lasers. Also the thinner the part the longer the measurement time, up to 60 seconds, making the acquisition vulnerable to environmental vibrations and air turbulence decreasing repeatability of measurements. 

Vibration Insensitive/Low Coherence

4D technology introduced a system to solve the long-standing problem of errors caused by vibrations in the machine and testing environment while minimizing coherent artifacts. They used a delay line and a synchronous translation of two components: the reference element and one of the mirrors in the delay line to achieve the vibration-insensitive performance in their model of the Fizeau interferometer. The drawback of such an approach was that it led to complicated architectural design.

Ring Source/Partial Coherence

ZYGO introduced the ring illumination system [ Küchel]. It is similar to a method used by Zeiss [Küchel] in their high performance interferometers. The ring increasingly lowers image artifacts contributions to the measurement the FARTHER the artifact is from image plane. So dust near the launch of the illumination beam is more suppressed than in the reference element. At catseye the ring must be reduced to a spot or no interference is observed due to the wavefront flipping. Similar approaches with a simple enlarged dot illumination are also utilized over shorter optical cavities. The dot could be considered temporally coherent and spatially incoherent.

2010’s – High Resolution Imaging, Low Retrace Errors and Spectral Source

CNC polishing machines require rapid and precise feedback between measurement results and fabrication processes. Ideally, an interferometer should be used in a closed loop as a guiding tool in the polishing operation; these needs drive the requirement for low retrace errors, low image distortion, high spatial resolution and acceptance of large departures from “null” condition.

New Interferometer Designs

The older systems, with Mark II™ legacy 6X zoom optics and intermediate fringe images projected on rotating ground glass disks, are inadequate to support CNC polishing applications. In response, 4D Technology and later ZYGO introduced high pixel count interferometers with better image resolution. These systems have better imaging and higher slope acceptance.

Äpre Instruments S-Series Interferometers

Äpre Instruments took interferometer design a step further with balanced optical designs.  The HR interferometers for computer controlled polishing applications and the SR interferometers for General Purpose optical shop testing, 

HR-High Resolution

ÄPRE S-Series HR interferometers for computer controlled polishing applications or where the highest image resolution and wavefront slopes are required.

  • Diffraction limited 2K X 2K spatial resolution (not just pixel count)
  • <0.1% image distortion
  • <λ/20 retrace errors at 500 fringes of tilt
  • Up to 650 fringes of slope across the aperture

SR – Standard Resolution

ÄPRE S-Series SR interferometers are for general purpose optical ship testing.  The SR finally replaces the 40-year-old Mark II optical design; outperforming the old design by large measure, without increasing the price to the user.

  • Diffraction limited 1K x  1K spatial resolution (not just pixel count)
  • <0.1% image distortion
  • <λ/20 retrace errors at 250 fringes of tilt
  • Up to 375 fringes of slope across the aperture

Surface of Interest Isolation

Spectrally Controlled Interferometry (SCI™)

ÄPRE has introduced a practical SCI source [Olszak], a new source modality to Fizeau interferometry. SCI controls the coherence, fringe position (over 100’s of millimeters) and phase modulation of the fringes electronically. SCI aligns in high coherence mode, like a laser, isolates like a white light source, positions the fringes within the cavity, and phase modulates regardless the cavity size, even down to 50um. By isolating the surface of interest, accuracy is improved and new applications are enabled. This is a new technology and its impact will emerge in the coming years.

Laser Fizeau compared to SCI Fizeau – 1 cm substate with 250 um step in the middle.

Delay Line Surface Isolation

4D Technologies introduced a light source based on a coupled delay-line to project low coherence fringes. Working in a plano-cavity it can place low coherence fringes a distance from the TF and move them over ~25 mm range. Isolating the surface of interest.

Appendix – Hidden Developments

Throughout the history there have been groups developing interferometers whose performance was never made public due to proprietary or classified project constraints, e.g. Perkin Elmer, ITEK, Zeiss, Nikon, Canon, Tropel, etc. Some of these systems were more advanced than available commercial systems, or even disclosed technology in open publications of the time.

Unfortunately these pioneers are not recognized in the open literature, but they too have significantly advanced the state-of-the-art of interferometry and optical manufacturing.

Fizeau Interferometer to Measure Precision Aspheres

 

Summary

The Fizeau interferometer has a long history and promising future. Interferometers will continue to evolve as applications and processes drive the need for change and new technologies enable these changes to be implemented.

Contact ÄPRE to discuss your interferometery needs to apply the best source + interferometer to your application. 

 

Note: We welcome your comments or additions to make this history more complete. 

Posted on

Laser Munich 2017

Jan Posthumas of LaserPeak (on left) and Don Pearson, ÄPRE’s VP Sales (on right)

Don Pearson, our VP Sales and Jan Posthumas, of LaserPeak (ÄPRE Representative) presented ÄPRE’s S100|HR interferometer in Munich this June. Once again we were pleased to meet with, and make new friends while co-exhibiting with the PTB’s HLEM (Hi-Level Experts Meeting) group.

Presented was the S100|HR, part of ÄPRE’s S-Series interferometers with diffraction limited imaging to 50 µm resolution (S50|HR), and all with <0.1% image distortion and <λ/20 retrace errors even at 6.5 fringes/mm.

We were also pleased with the interest in our new SCI based system that electronically remove back reflections from measurements and we look forward to discussing this more in the future.

 

 

Posted on

Fizeau Interforometer: To Zoom or Not to Zoom…

In this blog we explore the camera array size required to accurately measure Zernike polynomials in a laser Fizeau interferometer, and thus determine when a zoom system is important. (Hint: Zoom is a historical artifact)

Is a Zoom System Required?

Recently we were asked to provide a system with 4X zoom imaging to accommodate a 25 mm part in a 100 mm system. The thinking being to accurately measure a small part a zoom system is required. It is important to first understand what is the measurand, the quantity measured. In this case the customer wanted to measure and correct alignment errors as indicated by Zernike polynomial terms.

A zoom system adds complexity and cost, plus it can make calibrating the aperture size (pixel size) more complicated. A zoom also matches the image size to the camera, maximizing the pixel count active in a measurement. This raised the question, “How important is pixel count for measuring 36 Zernike terms accurately?” In this case accurate meant up to λ/10 P-V.

Camera Array Size Simulation

Using ÄPRE’s REVEAL software we simulated a measurement by building an artificial surface in the Zernike surface generator. The generator can be set for any pixel array size. Three pixel array sizes were simulated: 512 X 512 (1X zoom), 128 X 128 (4X zoom), and 64 X 64 (8X zoom). See figure 1 for examples of the 64 X 64 and 512 x 512 array data.

 

figure 1: Simulated data and represented in a 54 x 64 array (left) and 512 x 512 array (right)
figure 1: Simulated data and represented in a 54 x 64 array (left) and 512 x 512 array (right)

The input values of the 36 Zernike coefficients were compared to the calculated results for the three array sizes. These differences indicate the measurement uncertainty simply due to array size influences on the calculation of the Zernike polynomials.  

As can be seen in figure 2 the 64 X 64 array deviated up to 0.08 fringe (0.04 wave = λ/25). The 256 X 256 and 512 X 512 never induced errors no greater than 0.006 fringe!  Indicating arrays larger than 128 x 128 have no influence on the results.

figure 2: Reported result subtracted from input for up to 36 Zernike coefficients
figure 2: Reported result subtracted from input for up to 36 Zernike coefficients

Aperture Converter

To measure a part smaller than 25% of the aperture add an aperture converter to decrease the output aperture to match the smaller part. Caution: Adding an aperture converter can make the interferometer more sensitive to retrace errors in high slope measurements

Why Zooms?

Zoom systems were introduced in the late 1970’s when vidicon cameras were 64 X 64 or at best 128 X 128 effective array resolution. Beyond 2X zoom the Zernike terms started to fail and thus a zoom was needed. Continuous zoom systems were commercially available at 6X and thus 6X became the standard. After 35 years of use it is easy to assume a zoom imaging system is needed.

Conclusions

A zoom system (up to 8X zoom) is not required to “fill the camera array” to achieve results accurate to λ/25 when measuring up to 36 Zernike polynomial terms. The best configuration in this case is a fixed magnification system, optimized for the camera array to pass the maximum spatial frequencies.

Posted on

Vibration Tolerant Interferometry

This blog post discusses improvements in phase shifting algorithms for increased accuracy.

From the earliest days of phase shifting interferometry (PSI) phase ripple has been a problem. Ripple in the phase data follows the live fringe pattern but with twice the fringe frequency (ripple with the same frequency as the fringes can also appear and will be discuss at the end of the article). Ripple is an increase in measurement uncertainty (lower accuracy) and thus needs to be minimized. Further ripple can mimic mid-spatial frequency errors confusing the control feedback when spot polishing. Thus its minimization is important to good quality control.

Correcting Phase Ripple

In the late 1970’s Phase Ripple was called the “ripple bug” and its origin was unknown. The primary source was found to be vibration in the interferometer cavity during the data acquisition, and later other sources were identified such as nonlinearities in cameras and the phase shifting mechanisms.  Any deviation from equally spaced phase shifts during acquisition or non-linearities that distorted the shape of the fringes cause ripple to form. Cameras became more linear with the advent of the then new CCD’s, and control of phase shifting mechanics improved, yet vibration is always present.

Nulling the Fizeau Cavity to Minimize

The first technique to minimize ripple was simply to null the cavity. By minimizing the visible fringes, the ripple is spread across the data. If perfectly nulled the ripple is insignificant when the test surface is a perfect sphere. This is still good practice as a nulled cavity exhibits the least errors in a Fizeau interferometer. Yet it is not always possible to null the fringes and so ultimately a better approach was needed.

Improved Phase Shifting Algorithms

In the early 1980’s the standard phase algorithm was four camera frames (buckets) spaced by 90°. Jim Wyant pointed out that only three frames were required to find phase, but this algorithm is particularly vibration sensitive.  Four frame PSI, initiated by John Bruning’s group1, was less sensitive and in the late 1980’s Hariharan2 introduced a five frame PSI algorithm that was better than both. In 1988 Kathy Creath3 investigated numerous algorithms with varying sensitivity to ripple and in 1997 Peter Degroot4 wrote a “definitive” paper on phase shifting algorithms.  These approaches made PSI less sensitive to phase shift spacing and the jitter between phase frames, but did not directly address the unequally spaced fringes due to vibration.

New Approach: Post Acquisition Correction

Ripple in Phase Data and Corrected with Äpre Universal Phase Algorithm

In 1982 Morgan5 investigated applying a post acquisition least squares correction to PSI. In the 1990’s a parallel line of investigation became active. This approach corrects the acquired data to the expected phase shifts through mathematical optimization.  I.Kong and S. Kim 6,7 created a least squares PSI algorithm and an algorithm to “automatically suppress phase shift errors”, followed by C.Wei, M. Chen, & Z. Wang 8 with a “General Algorithm for phase-shifting interferometry by iterative least squares fitting”. Over the next 10 years a flurry of work 9,10,11,12,13,14,15 developed algorithms immune to translational and in some cases tilt shift error using iterative optimization. These works established the methodologies for vibration tolerant algorithms and demonstrated that with fast computers phase shifting errors could be minimized algorithmically, and practically.

Commercially Available Today

Vibration tolerant PSI, based on 35 years of development, are now commercially available as found in ÄPRE’s “Universal Phase Algorithm”6 in REVEAL™. The universal phase algorithm effectively minimizes phase ripple, as long as the vibration does not exceed ~150 nm P-V (λ/2 fringe). If the vibration exceeds 150 nm P-V then phase shifting interferometry breaks down and simultaneous PSI (Multi-Camera or Carrier Fringe) is required.

Vibration is not the only source of phase ripple

Intensity Variations

When phase ripple appears at the same frequency as the fringes illumination intensity variation during measurement is a likely cause. This can occur due to a laser or light level control failing. Interestingly, in interferometers equipped with rotating diffusers, variations in light level may occur due to differences of transmissivity in different areas of the diffuser rotating disk or simply by dirt on the diffuser disk.

Fringe Contrast Variations

Fringe contrast (modulation) is generally defined by the coherency of the source and is usually quite stable. However a laser can exhibit variations when the source is not properly stabilized. Also laser instability can be caused by mechanical vibrations when combined with long exposure times (usually longer then 10 ms.). In the later case the moving fringes will “average out” over a small area causing a loss of modulation that may be different for each recorded fringe image. The combination will create phase ripple in the data.

Tilt Variations

Vibration is considered a “piston” term – equal for every pixel across the aperture. If the phase shifting mechanics do not move straight the phase shifts will vary across the aperture, causing uncorrected ripple even with a correction algorithm. Recent work9,14 has attempted to address this error. This tilt induced ripple can also occur if the test or reference is not rigidly mounted.

Test or Reference with High Reflectivity

When one of the test parts has a high reflectivity fringes are detected that have reflected several times within the cavity. These multiple reflections distort the fringe shape. PSI algorithms, including vibration tolerant algorithms expect sinusoidal fringes. The distorted fringes are non-sinusoidal and induce phase ripple. To suppress the multiple reflections special coatings are applied to the reference or a thin pellicle is placed between the test and reference to suppress the multiple reflections.

References:

  1. J. H. Bruning, D. R. Herriott, J. E. Gallagher, D. P. Rosenfeld, A. D. White, and D. J. Brangaccio, “Digital Wavefront Measuring Interferometer for Testing Optical Surfaces and Lenses”, Appl. Opt. 13, 11, 2693-2703 (1974)
  2. P. Hariharan, B. F. Oreb, and T. Eiju, “Digital phase-shifting interferometry: a simple error-compensating phase calculation algorithm”, Appl. Opt. 26, 13 2504 – 2506 (1987)
  3. K. Creath, “Phase-shifting interferometry techniques,” Progress in Optics, E. Wolf, ed. (Elsevier, 1988), Vol. 26, 349-393
  4. P.Degroot, “101-frame algorithm for phase shifting interferometry”, Europto 1997, Preprint 3098-33
  5. C.J.Morgan, “Least-squares estimation in phase-measurement interferometry”, Opt. Lett. 7, 368-370 (1982)
  6. I.B.Kong & S.W.Kim, “General Algorithm for phase-shifting interferometry by iterative least squares fitting”, Opt. Eng. 34, 183-187 (1995)
  7. I.B.Kong & S.W.Kim, “Portable inspection of precision surface by phase-shifting interferometry with automatic suppression of phase shift errors”, Opt. Eng. 34, 1400-1404 (1995)
  8. C.Wei, M. Chen, & Z. Wang, “General phase-stepping algorithm with automatic calibration of phase steps,” Opt. Eng. 38, 1357-1360 (1999)
  9. Chen, Guo and Wei, “Algorithm immune to tilt phase-shift error for phase-shifting interferometers”, Appl. Opt, 39, 22, 3894 – 3898 (2000)
  10. K.G.Larkin & B.F.Oreb, “Design and assessment of symmetrical phase-shifting algorithms”, J. Opt.Soc.AM. A 9, 1740-1748 (1992)
  11. K.G.Larkin, “A self-calibrating phase-shifting algorithm based on natural demodulation of two-dimensional fringe patterns”, Opt. Expr.9, 236-253 (2001)
  12. H.Guo & Z.Zhang, “Phase shift estimation from variances of fringe pattern differences”, Appl. Opt. 52, 26, 65726578 (2013)
  13. Y-C Chen, P-C Lin, C-M Lee, & C-W Liang, “Iterative phase-shifting algorithm immune to random phase shifts and tilt”, Appl. Opt. 52, 14, 3381-3386 (2013)
  14. M.Wielgus, Z. Sunderland, K. Patorski “Two-frame tilt-shift error estimation and phase demodulation algorithm”, Opt. Letters 40, 3460-3463, August 1 2015
  15. L. Deck, “Model-based phase shifting interferometry”, Appl. Opt. 53, 4628-4636, July 2014
  16. P. Szwaykowski, “Minimization of vibration induced errors using a geometrical approach to phase shifting interferometry”, ASPE Summer Conference on Interferometry, July 2015
Posted on

Fizeau Interferometer: Buy or Upgrade; what are the purchasing options?

Fizeau Interferometer Buyers Guide 9

This blog is about the performance and price options for laser Fizeau interferometers

Up to this point we have been discussing how various applications require specific interferometer sensor configurations and features. Now comes the key point when you need to do something. Do you need increased production capacity? Has a new process been introduced that requires better feedback? Is the IT department concerned about an old operating system? Has the computer failed, or the system has become unreliable but meets your production needs? Do you have a new program that requires a dedicated system? Or your customer is pushing for a result your system does not produce. What do you do? Do you buy a new interferometer? What are the options?

Buy New, Upgrade or Buy Refurbished?

Asking some questions can lead you to the purchasing options to consider.

  1. Is the system to support a spot polishing process where slopes and mid-spatial frequencies are important?
    • Yes – indicates a high performance imaging interferometer with a 2K X 2K level camera, low distortion and low ray-trace errors.
  2. Is the environment harsh, with vibration and air turbulence present?
    • Yes – indicates a SPMI (Multi-detector or Carrier Fringe acquisition) system
  3. Does your application require custom fixturing, a special wavelength or non-standard aperture?
    • A custom system is required – talk to the various providers regarding your best option
  4. Does the system support a standard lap polishing process where form is the key measurand?
    • Yes – indicates a classic interferometer

High Performance Imaging System laser Fizeau

These are the latest technology and will meet all the requirements for most situations, the problem is they tend to be expensive. Not only do they image mid-spatial frequencies well, the associated low ray trace errors mean they are suitable for carrier fringe data acquisition for operation in harsh environments. The major drawback is price. Most systems are 1.5X to 2X more expensive than a classic interferometer. If they were the same price everyone would probably buy one of these interferometers.

Harsh Environment laser Fizeau or laser Twyman-Green

There are several interferometers available that meet this need using both carrier fringe and multi-camera or multi-pixel configurations, Many of these applications have specific specifications that dictate size, weight, and result output. It is best to discuss these with the manufacturer to arrive the best choice.

Classic laser Fizeau Interferometer

With the classic Fizeau there are the most choices.

Refurbished miniFIZ interferometer
Refurbished miniFIZ interferometer

Buy New or Refurbished: Increase Production Capacity

If increased production capacity is required there are two choices: Buy new or refurbished. There are a few choices for new systems that have the same optical system as produced for the last 30 years – with extensively upgraded software! These new system are priced between $60,000 and $75,000 (USD).

Also available from time to time are refurbished interferometers with the same/similar classical optical design. These refurbished systems have the latest data acquisition and analysis software like a new system and are priced between $33,000 and $37,000.

Upgrade: Failed System, Old Operating System, New Acquisition and Analysis Software Required

There are thousands of interferometers installed worldwide that can be renewed by upgrading the electro-optics and software. These systems can operate as well as a new system, with the latest software, cameras and computer systems. Upgrading is cost effective and is priced between $22,000 and $27,000. Upgrading is usually the best choice when production capacity is not an issue, but systems are down. A side benefit is the increased efficiency of new electronics can also increase the throughput and therefore production capacity of existing systems.

Summary

There are several purchasing options available regarding laser Fizeau interferometers. Applications often drive the decision but price is also important.laser Fizeau Relative Pricing

Posted on

Measuring Thin Parallel Plates – Buyers Guide Chapter 8

In this blog the measurement of thin parallel plates with a Fizeau interferometer is discussed.

Filters, etalons and plane parallel components exhibit reflections from the front and back surface rendering them impossible to measure in a standard laser Fizeau interferometer. A standard interferometer uses a laser, making interference easy to create, no matter the interferometer cavity length. With parallel plates additional interferometer cavities are created adding confusing fringes: 1) Reference surface to the plate front surface, 2) reference surface to the plate back surface and 3) plate front surface to back surface.

A few techniques are available to overcome this confusion.

Spectrally Scanned Interferometry (SCI) – Click for more information

Laser Fizeau compared to SCI Fizeau – 1 cm substate with 250 um step in the middle.

ÄPRE has introduced a practical SCI source, a new source modality to Fizeau interferometry. SCI controls the coherence, fringe position (over 100’s of millimeters) and phase modulation of the fringes electronically. SCI aligns in high coherence mode, like a laser, isolates like a white light source, positions the fringes within the cavity, and phase modulates regardless the cavity size, even down to 50um. By isolating

the surface of interest, accuracy is improved and new applications are enabled. This is a new technology and its impact will emerge in the coming years.

Wavelength-Modulation + Fourier Analysis

Modulating laser wavelength will change the observed phase of the interference fringes.  The rate of fringe modulation as the wavelength is changed is a function of the interferometer cavity length, long cavities modulate more rapidly than short cavities.  Thus when a wavelength scan is performed and the results Fourier analyzed for modulation frequency the various cavities can be separated. By performing phase shifting interferometry analysis on the now separated surfaces thin parts can be measured, surface by surface. The drawbacks of this approach tend to be price and careful set up. To assure proper extraction, the surfaces must be positioned so the modulations are separable and not overlapped which is not always possible. Some versions also provide absolute position in space enabling millimeter length steps to be measured. 

Short Coherence Balanced Arms

An incoherent source, like a diode, can produce fringes at a location in front of a Fizeau reference flat IF a secondary interferometer system is coupled to it. By adjusting the coupling cavities length the interference fringes are placed in space in front of the Fizeau reference surface. This method produces high quality, single surface fringes where the front and back surfaces of a thin part can be measured. Another short coherence approach is to use a Twyman-Green equal path interferometer and a diode. The main drawbacks of these systems are price and set up. The fringes exist at a specific point in space and the test part must be moved to within micrometers in tip and tilt and Z to simply see fringes. This can be challenging if separate alignment aids are not provided.

Grazing Incidence

By producing a steeply grazing illumination beam and varying the spatial coherence of the illumination, the back surface of a thin part can be eliminated from measurement. This techniques has been used successfully to measure semiconductor masks and sapphire wafers, though it is not used often in optical testing. The steep grazing incidence angle enable even rough surfaces to reflect specularly, with desensitized fringes (5um equivalent wavelength) and therefore the accuracy is not sufficient for most optical work. 

 

Posted on

Measuring Steep Sphere and Asphere Surfaces – Buyers Guide Chapter 7

In this blog the measurement of steep spheres and aspheres with a Fizeau interferometer is discussed.

Steep Convex Spheres – Stitching

A limitation of Fizeau interferometry is the inability to measure steep convex spheres with f#’s beyond the reference surface f#. This is a severe limitation for spot polishing machines that require data across the entire surface to apply the necessary corrections. The solution is a stitching system that acquires sub-apertures across the partially covered surface and mathematically combines them into a complete surface. Stitching includes matching overlapping areas for tips and tilts, and sometimes distortions and rotations and is not a simple image stitch. Several manufacturers now offer these systems.

Stitching can introduce errors. Stitching errors are found in the lowest spatial frequencies, particularly power. A simple test for errors in power is the measurement of radius of curvature. Measure a part’s radius of curvature across the vertex sub-aperture and compare this value to the radius of curvature measured across the entire stitched surface. The difference of these two includes the stitching errors, plus the reproducibility of the two radius of curvature measurements. Measuring radius of curvature is challenging and careful metrology practice must be followed to confirm this test. To assess surface irregularity accuracy compare a surface measured with a f/0.75 Transmission Sphere (Fizeau reference) and the same surface area stitched with a

n f/3.3 Transmission Sphere. Best is subtracting the two measurements from each other to highlight the stitching errors, though this is not always easy to implemented due to differing data set sizes. Stitching systems by leading manufacturers appear to have solved these problems, yet understanding potential limitations is important.

A “lattice” of subapertures covers the full aperture of high-numerical-aperture and large-clear-aperture parts1

The major limitations now seem to be cost and speed of measurement.

 

Asphere Metrology

Aspheres are difficult to measure with Fizeau interferometers.  A Fizeau operates best when the surface is a nulled sphere to minimize ray-trace errors, and aspheres can greatly deviate from a sphere. Further the high slopes of aspheres can exceed the slope limit of the imaging system causing the measurement to fail. Multiple approaches to overcome these limitations are used.  

Asphere Stitching

Just like spheres an asphere stitching system builds up the surface by measuring sub-apertures. This is more difficult than measuring a sphere as the ray-trace errors will exist in each sub-aperture which must be minimized, or calculated and removed. With steep aspheres even the sub-apertures exhibit slopes exceeding the imaging limit of the interferometer. Complicated compensation techniques (such as rotating wedges) are used to minimize measured slopes, requiring mathematically correction for ray-trace errors, and induced distortions of the variable compensating wedges. Measurement time (>30 minutes) and cost tend to be the major concerns for these systems.

Measurable aspheres are limited to near axially symmetric surfaces with nominally monotonically increasing curvature. Reversed curvature (gull wing) aspheres are not measurable with these systems.

Asphere Scanning Fizeau

Scanning Fizeau zones2

Scanning Fizeau is similar to stitching systems, but scan only in Z, along the parts optical axis. Rings of data paired with the caustic zone Z is compared to the expected Z position and surface surface shape. Since data is acquired at the null of each ring, ray tracing errors are minimized, for low measurement uncertainty. These systems have been used with picometer measurement uncertainty for semiconductor lithography optics asphere manufacture.  Limitations due to the reference sphere f# and surface curvatures exist limiting its application to specific lens types. Since a full ring of data is measured these systems tend to measure an entire surface in <5 minutes.

Scanning Fizeau systems promise high accuracy with fast data acquisition. Yet measurable aspheres are limited to near axially symmetric surfaces with nominally monotonically increasing curvature. Reversed curvature (gull wing) aspheres are not measurable with these systems.

Asphere Sub-Nyquist Fizeau

Sub-Nyquist has existed since the 1980’s but only recently introduced commercially. This system pinhole masks the detector allowing fringes beyond the nyquist limit to be detected and thus acquired. 

(a) SNI Fringe Pattern, (b) PSI reconstruction, (c) SNI reconstruction3

Sub-nyquist fringes by nature are highly tilted, introducing errors that vary from measured part to measured part. These ray-trace errors are calculated and removed mathematically considering both the interferometer optical design AND the part under test. Mathematical ray-trace error removal demands full knowledge of the interferometer optical design, as manufactured, and its sensitivity to varying environmental influences. For this reason sub-nyquist accuracy can be considered limited to commercial grade parts. Sub-nyquist promises fast measurement (<3 minutes) on a limited set of surfaces with limited accuracy.

Sub-nyquist Fizeau promises fast data acquisition with the ability to measure non-axially symmetric surfaces with nominally monotonically increasing curvature. Reversed curvature (gull wing) aspheres are not measurable with these systems.

Tilted Wave Interferometer for Asphere Measurement

A new entrant into asphere metrology is the tilted wave interferometer. In development for the last 10 years the tilted wave promises high speed metrology of asphere surfaces. By moving the source position multiple areas of an aspheric surface can be acquired and then analyzed. The tilted wave can be thought of as a stitching interferometer (without the motion) and yet requires a sub-nyquist type of calibration for every point in the measurement VOLUME.

Tilted wave setup & zone distribution for asphere test piece4

Each point in the measurement volume must be calibrated for each transmission element. These calibrations can be temperature dependent and a function of the manufacturing tolerances. Calibration of the actual system is required and most likely on a repeated basis. This type of system seems close to commercialization and it will be interesting to learn of its measurement uncertainty, correlation to other technologies, speed of measurement (one of it proposed benefits) and cost.

Fizeau Interferometer Limited to Near Axially Symmetric and Monotonically Curved Aspheres

In all cases applying Fizeau interferometers to aspheric surfaces extends its capabilities to perform outside its “sweet spot”. Mathematical combinatorial techniques along with extensive “calibrations” achieve acceptable measurement uncertainty.

Even with these impressive innovations non-monotonically varying slopes and non-axially symmetric surfaces are a major limitation for Fizeau interferometers, especially if the surface reverses curvature relative to the base sphere. In these cases the reflected light does not enter the interferometer and the surface is not measurable. This is especially true for gull-wing and sombrero lenses and free form surfaces which cannot be measured with Fizeau interferometers. This is not to say that modified Fizeau interferometers don’t have their place regarding aspheres. The main benefit, when they are applicable is higher spatial resolution in an acceptable time period compared to stylus profilers. For general purpose measurement of the wide range of potential surface shapes is needed and when a high resolution or 3D image of the surface is not required, contact stylus and optical stylus systems are favored for asphere metrology.

Final Word

Though not generally considered an interferometer, the Luphos optical probe is a single point, multi-wavelength Fizeau interferometer.

Single point multi-wavelength Fizeau interferometer5

It has the same limitations as all Fizeau interferometer with two benefits: Absolute position sensing and single point. The absolute positioning allows the probe to sense a position in space to nanometers within a few millimeters. Thus if the probe “falls off” a part it can regain position, depending on the stability of the metrology frame. Being single point, if the metrology frame and positioning system support the motions the probe can follow non-rotationally symmetric surfaces and potentially reversing curvature (gull-wing) parts. Thus it is more general purpose, and like any other stitching system can measure steep surfaces. Just like any Fizeau, deviations from measuring off the surface normal produce two errors: The signal can be lost if no light returns and ray-tracing errors occur in the probe degrading performance. These errors are accommodated by adding a B axis to an XYZ positioning system. The more complex motion of a B axis requires careful calibration to achieve 50 nm level performance.

 

Next post: Thin plates measurement

1 A. Kulawiec, “Extended Aspheric Measurement Capability with Subaperture Stitching Interferometry”, http://www.photonics.com/Article.aspx?AID=34816

2 M Küchel, “Interferometric measurement of rotationally symmetric aspheric surfaces”, Proc. of SPIE Vol. 7389 738916-1

3J. Greivenkamp ; A. Lowman and R. Palum”Sub‐Nyquist interferometry: implementation and measurement capability”, Opt. Eng. 35(10), 2962-2969 (Oct 01, 1996)

4 E. Garbusi, C. Pruss, J. Liesener, W. Osten, “New technique for flexible and rapid measurement of precision aspheres”, Proc. of SPIE Vol. 6616, 661629, (2007)

5 G.Berger, J. Petter “Non-contact metrology of aspheric surfaces based on MWLI technology”, Proc. SPIE 8884, Optifab 2013, 88840V (September 6, 2013)

Posted on

Photonics West 2016

Zygo® GPI™ Upgrades Introduced

The First Phase Measuring Interferometer at Bell Labs

At Photonics West we introduced a new product, upgrading Zygo® GPI™ and Mark IV™ interferometers. This also includes the VeriFire™ line of interferometers. All these system are basically the same with minor variations and which we can accommodate.

We are pleased by the growing excitement about our ÄPRE REVEAL™ software. Its backward compatibility with MetroPro® file types and unique traceable metrology make it the production software of choice.

Also several other exhibitors displayed products run by REVEAL. Davidson Optronics again displayed their 12″ Fizeau interferometer, designed in concert with Äpre Instruments, along with the PSM micro-profiler both using REVEAL. M3 displayed their new 3.39um IR interferometer using REVEAL software.
See you in Frankfurt at Optatec 2016.®™

Posted on

Harsh Environment Testing: Optical Towers and In-situ Metrology – Buyers Guide Chapter 6

In this blog measurement of optics in a harsh environment with a Fizeau interferometer is discussed.

For large systems, typically telescopes, vibration and air turbulence hinder or prevent the measurement phase by temporal phase shifting. Also interferometers placed on machine tools to measure in situ experience a vibrating environment. When vibration and turbulence hinder measurement then only a simultaneous phase measuring system (SPMI) will be able to acquire data. These systems acquire phase data fast enough to freeze fringe motion due to vibration and turbulence.

SPMI Data Acquisition: Multi-Camera and Carrier Fringe

There are two primary SPMI data acquisition architectures: Multi-camera1  and carrier fringe2 .  Multi-camera uses polarization to split the intensity data into multiple images with shifted phases which are analyzed for wavefront phase.  Carrier fringe uses tilt in the wavefront coupled with several different analytical approaches to extract phase. Both approaches are successfully employed commercially, and are functionally and performance equivalent.

Tower for testing large mirrors at the University of Arizona

Averaging is Required

The SPMI system enables phase to be acquired, but the phase is changing rapidly and by large amounts and any single measurement is meaningless. To achieve stable data, averaging must be employed. The amount of averaging required is a function of the frequency and amplitude of the vibration and turbulence. A useful method to determine how much averaging is required is to acquire 100 data sets in a series as would be performed in an average. Calculate the RMS or P-V of this data set, divide the RMS or P-V by the measurement repeatability desired to obtain a ratio.  Square this ratio and set the average to this squared value.  For example, if the single measurement repeatability is 6,000 nm P-V and desired is 60 nm P-V then 1002 averages must be taken, at a minimum, to achieve 60 nm P-V repeatability, assuming a gaussian distribution.  It is often practical to stir the air with a fan to improve convergence, which can take many hours for large cavities with slowly moving fringes. SPMI systems can often acquire and calculate phase in seconds so averaging can be rapid.

Repeatability is Not Accuracy

Finally, note that repeatability is not low measurement uncertainty, or accuracy.  Measurement uncertainty is primarily driven by the optical design of the interferometer, temperature variations in all the optics, mechanical stresses in mountings and optical misalignments and null lenses errors – a la Hubble. Controlling these is much harder than averaging and is a topic unto itself.

SPMI Interferometers are Non-Common Path – Hence Lower Accuracy

Also note SPMI systems are non-common path systems – the polarization paths are different or tilt exists between the test and reference wavefronts. These differing paths degrade the optical performance compared to PMI which can be common path, i.e. the test and reference beams perfectly overlap when a sphere or flat is measured in a nulled condition. So from an accuracy point of view PMI- nulled can outperform SPMI, but when data cannot be acquired due to turbulence or vibration then SPMI is required and an accuracy compromise is acceptable.

Summary

Acquiring data in harsh, vibrating and turbulent environments requires an SPMI data acquisition interferometer. Achieving high accuracy results requires careful attention to the all measurement parameters and is typically of lower accuracy than a nulled laser Fizeau phase shifting interferometer in a quiet  environment.

1 Smythe, R & Moore, R; “Instantaneous Phase Measuring Interferometry”, Opt Eng, Jul/Aug 1984, 25(4):361 – 364

2 Takeda, M. “Spatial-carrier fringe-patter analysis and its applications to precision interferometry and profilometry: an overview, Ind Metrol 1990;1(2):79-99